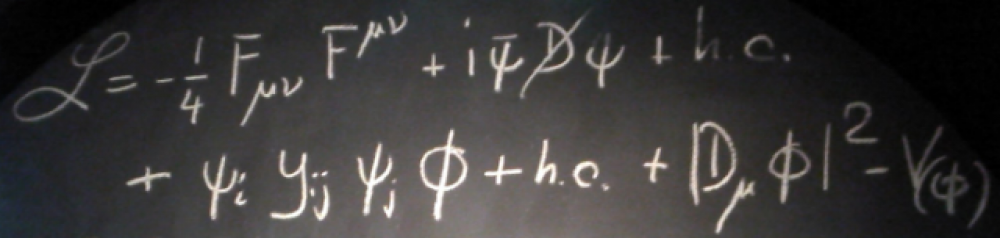Synopsis: This will be an introductory course on quantum field theory, focusing on particle physics and relativistic applications, though some of the tools may also be applied to condensed matter systems. The level will be aimed at 3rd/4th year Physics students, so there will be revision lectures to set the notation and background on quantum mechanics and special relativity.
The bulk of the course will then be to detail the canonical quantisation of relativistic fields, focusing mostly on the scalar and Dirac fields with a strong emphasis on examples. Exercise sheets will be provided.
Lecturer: Marco O.P. Sampaio, Physics Department Office 13.3.31.4
Location & schedule: Room 22.3.21 Mechanical Engineering Department, weekly on Wednesday at 15.00. Each session is 45min + 45min with a short break.
SUMMARIES:
Lecture 0 (3rd Oct 2012) "Introduction and motivation": In this lecture we have reviewed some arguments based on scales, which motivate the introduction of Quantum Field Theory at speeds compared to that of light (highly relativistic) and very short distances (highly quantum mechanical regime). We have also briefly looked at a summary of the Standard Model as a motivation to study QFT.
Lecture 1 (10th of October) "Revision of Special Relativity 1": In this lecture, we have looked at the Newtonian equations of Mechanics (invariance under Galilean transformations, translations and Rotations) and Maxwell's theory of light as a wave, as well as the Michelson-Morely experiment, to motivate the rupture with the Galilean transformations. Then we have looked at the postulates of special relativity and derived Lorentz transformations from the postulates, introducing the index notation and Minkowski space.
Recorded Lecture: Part 1, Part 2. Alternative formats: Part1, Part2 or Part 1, Part2
Lecture 2 (17th of October) "Special Relativity 2 & Lagrangian formalism": In this lecture we have looked at space-time diagrams and the laws of relativistic Mechanics for a single particle, and for a system of particles in a collision as to obtain conservation of 4-momentum. Then we have started looking at the Lagrangian formulation of Mechanics and Hamilton's principle.
Recorded Lecture: Part 1, Part 2 . Alternative formats: Part 1 , Part 2 or Part 1, Part 2
Lecture 3 (24th of October) "Lagrangian formalism & Revisions of Quantum Mechanics": In this lecture we have revised Hamilton's principle and the variational formulation of lagrangian mechanics. We have also summarised the Hamiltonian formulation of Mechanics and briefly revised the postulates of Quantum Mechanics.
Recorded Lecture: Part 1, Part 2 . Alternative formats: Part 1 , Part 2 or Part 1, Part 2
Lecture 4 (31st of October) "Bra/Ket formalism & the quantum harmonic oscillator": In this lecture we have detailed the quantum harmonic oscillator both in the space representation, as well as in the algebraic Bra/Ket formulation of Quantum Mechanics.
Recorded Lecture: Part 1, Part 2 . Alternative formats: Part 1 , Part 2 or Part 1, Part 2
Lecture 5 (7th of November) "Classical Scalar Field theory & Noether's theorem": In this lecture we have described the ideas of using field theory to describe a multi-particle theory. Then we have started discussing relativistic fields in light of their Lorentz group representations, derived the corresponding Euler-Lagrange equations of motions and proved Noether's theorem with some examples highlighting the important correspondance between symmetries and conserved quantities.
Recorded Lecture: Part 1, Part 2 . Alternative formats: Part 1 , Part 2 or Part 1, Part 2
Lecture 6 (21st of November) "Free solutions of scalar field theory and their canonical quantisation": In this lecture we have first derived the canonical energy momentum tensor in classical Lagrangian field theory, and have identified the time/time component with the Hamiltonian of the system. Then we studied the classical free field solutions of the Klein-Gordon equation and finally, started to describe the canonical quantisation of such a (free) theory.
Recorded Lecture: Part 1, Part 2 . Alternative formats: Part 1 , Part 2 or Part 1, Part 2
Lecture 7 (28th of November) "Spectrum & physical interpretation of free scalar theory. Heisenberg & interaction picture": In this lecture we have derived the energy spectrum of the states of the free quantised scalar field theory. Then we looked at observables and analysed the possible processes in the free theory. We concluded by revising the Heisenberg picture of quantum mechanics applied to field theory.
Recorded Lecture: Part 1. Alternative formats (note: part 2 was not recorder -- see lecture notes instead): Part 1 or Part 1
Lecture 8 (12th of December) "Perturbative interactive QFT and Wick's theorem": In this lecture we have defined the interaction picture, as a way to expand around the free scalar field theory. We have obtained the general scattering matrix solution and started proving Wick's theorem for the product of field operators.
Recorded Lecture: Part 1. Alternative formats: Part 1 or Part 1
Lecture 9 (16th of January 2013) "Wick's theorem and Feynman rules": In this lecture we have completed the derivation of the Feynman rules for correlation functions in scalar phi^4 theory in real space and momentum space.
Recorded Lecture: Part 1. Alternative formats: Part 1 or Part 1
Lecture 10 (23rd of January 2013) "Feynman rules for scattering & cross sections": In this lecture we have discussed vaccum bubbles and how to obtain physical interacting states from the interaction picture physical states. Then we have formulated the Feynman rules for scattering processes which are central to the computation of experimental interaction cross sections in particle physics.
Recorded Lecture: Part 1. Alternative formats: Part 1 or Part 1
Lecture 11 (30th of January 2013) "Particle Physics examples & final Summary": In this lecture we have presented some examples of calculation of matrix elements within scalar theories and the connection with the scattering cross section that can be measured experimentally. We finished the course with a summary of the topics that were covered commenting that could be covered beyond the course as a complement.
Recorded Lecture: Part 1. Alternative formats: Part 1 or Part 1
Attachments: